Abstract
The accumulation of organic compounds associated with plastic materials into pharmaceutical products and their associated solutions has important suitability for use consequences for those pharmaceutical solutions, most notably in terms of safety and efficacy. The interaction between the pharmaceutical solution and the plastic material is driven and controlled by the same thermodynamic and kinetic factors that regulate the interaction between the constituents of any comparable two-phased system. These physiochemical factors are delineated in this article, and their application to pharmaceutical products is demonstrated.
LAY ABSTRACT: When drug products are packaged in plastic container systems, substances may leach from the container and accumulate in the product. The magnitude of this leaching, and thus the effect that leachables have on the drug product, is controlled by certain thermodynamic and kinetic processes. These factors are described and detailed in this article.
Introduction
Plastic materials are used in the production, packaging, and delivery (administration) of pharmaceutical products and their associated process solutions. The composition and processing of these materials give them their necessary and desirable physical performance characteristics. The composition and processing of the materials also affect their interactions with those pharmaceutical solutions that they come in contact with. One such interaction is the migration or leaching of organic constituents of the plastic material into the product (or solution), which is relevant because the extent of leaching can impact the product's suitability for use, specifically with respect to safety and efficacy.
The interaction between a plastic material and the product or solution that it contacts is governed by the same thermodynamic and kinetic physiochemical processes that govern the interaction between any two immiscible phases. Understanding these processes, and the contact variables that affect them, can facilitate the design and interpretation of efficient and effective extractables and leachables assessments. For example, such an understanding may allow for the identification and justification of solvents to simulate a particular drug product, thus facilitating for the extrapolation of extractables assessments to leachables scenarios. Similarly, such an understanding may be useful in interpreting, and even predicting, extractables and leachables accumulation levels and trends.
This article outlines these physiochemcial processes in terms of their influence on material–solution interactions and establishes how they are affected by the nature of the solution, the nature of the material, and the conditions of contact. Both thermodynamics, which defines the absolute maximal equilibrium interaction between a material and a product, and kinetics, which defines the rate at which the interaction occurs, are considered. This article expands on the general concepts discussed in a previous manuscript (1), considering such concepts in greater detail, expanding the concepts to include additional considerations and providing additional examples that further illustrate the application and utilization of these concepts.
Thermodynamics of Partitioning
General
The equilibrium distribution of a compound between two immiscible phases (phase 1 and phase 2) is defined by the distribution, or partition, coefficient, P, which is the ratio of the compound's equilibrium concentrations (C) in the phases:

When the phases have the same nature (e.g., both are liquids), their units of concentration are the same and they cancel, making P dimensionless. However, the convenient concentration units for a system consisting of a plastic and a solution differ. For example, solute concentrations in a plastic material are typically expressed on a weight basis (e.g., micrograms per gram [μg/g], parts per million [ppm]) while solute concentrations in solution are typically expressed on a volume basis (e.g., micrograms per milliliter [μg/mL], ppm). These mixed concentration units can be addressed by converting solution concentrations from liquid to mass units via the density. If the solution's density is approximately 1 g/mL, the term equilibrium interaction constant Eb has been used to express the relationship between Cp and Cs:

In this equation, Cp is in units of mass (e.g., μg/g]) and Cs is in corresponding units of volume (e.g., μg/mL]).
The Eb value, coupled with the material weight (Wm, in grams), the solution volume (Vs, in milliliters) and the total pool of a compound in a material (Tp, in μg/g), can be used to calculate the partition-mediated equilibrium concentration of that compound in a solution in contact with a material (2):
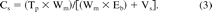
Use of this equation is illustrated as follows. An additive is present in a plastic at a concentration of 3000 ppm (μg/g). This value is Tp. If the weight of the plastic used is 20 g, the solution volume is 250 mL and the additive's Eb = 200 (the additive is 200 times more likely to be in the material versus in solution), then the concentration of the additive in the solution is calculated as follows:
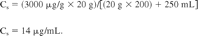
The use of this equation to estimate leachable accumulation levels is constrained by the limited amount of published Eb data. This shortcoming can be mitigated, however, if one recognizes that the partitioning of a solute between a plastic and a solution is essentially the same physiochemical process as the partitioning of a solute between an organic solvent and a solution. If an organic solvent can be identified that exhibits the same partitioning behavior as the plastic material and if the solute's solvent/solution partition coefficient is readily available, then the solvent/solution partition coefficient could be used in place of the material/solution coefficient and eq 3 could be generally applied.
Although it is clear that plastics are not specifically polymerized from solvents like octanol and hexane, it has nevertheless been demonstrated that materials used in pharmaceutical applications exhibit octanol-like and/or hexane-like partitioning behavior. The octanol/water partition coefficient (Po/w) is readily available for many compounds because this property has been correlated to many important behavioral characteristics such a solubility, bioavailability, environmental fate, and others. Partition coefficients for other solvent/water systems (e.g., hexane/water) are less frequently known or available. Relationships between a plastic/water Eb and solvent/water partition coefficients (such as Po/w) have been developed and published for several plastics (3–5) and generally take the form
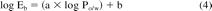
where the coefficients a and b are established experimentally. For instance, the following relationship between Eb and Po/w has been established for a multi-layer polyolefin laminate material that could be used, for example, as a primary container for aqueous drug products (6):
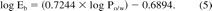
If octanol was an exact model for this material, then in essence Eb and Po/w would have the same magnitude (allowing for differences in the units in which they are measured) meaning that the slope of eq 5 would be one and the intercept would be zero. The less-than unit slope of eq 5 indicates that the plastic material is less responsive to differences in compound properties (like polarity) than is octanol and the negative intercept indicates that the plastic material has an intrinsically smaller interaction capacity than does octanol.
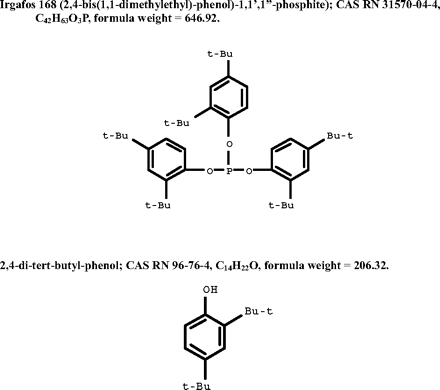
The use of eq 5 can be demonstrated by re-examining the previous example of the 20 g material and the 250 mL of solution. If this material is the one for which eq 5 was generated, eqs 3 and 5 could be used to estimate leachables accumulation levels for a material additive such as Irgafos 168, a commonly employed antioxidant (trade name for a material sold by Ciba Specialty Chemicals, CAS registry number 31570-04-4; see Figure 1 for chemical name and chemical characteristics). The log Po/w value for Irgafos 168 is 13.7 (7), which produces an Eb value of 1.7 × 109 per eq 5. Insertion of this Eb value into eq 3 results in an estimated equilibrium concentration for Irgafos 168 of considerably less than 1 ppb (μg/L).
Leachables considered in the thermodynamic example; Irgafos 168 and its related degradation product.
Given this low accumulation level, one would conclude that Irgafos 168 itself has no direct impact on product safety or efficacy. However, such a conclusion would not take into account its potential indirect impact. Because Irgafos 168 is an antioxidant, it is reasonable to expect that it degrades while the plastic is manufactured and when the manufactured part is used in conjunction with the pharmaceutical product. Such degradation products, which would be lower in molecular weight and more polar than Irgafos 168, could be leachables that accumulate at higher levels than the Irgafos 168 itself. For example, 2,4-di-tert-butyl-phenol (Figure 1) is a known Irgafos 168 degradation product which has been reported as a leachable from polyolefin materials. The reported log Po/w for this compound is 4.61 (7), considerably lower than that of Irgafos 168. Substitution of this value into eq 5 produces an Eb for this compound of 450.
In order to calculate the solution concentration of this degradate, its total pool in the plastic must be known. Its worst-case pool would be 3000 μg/g, based on the unlikely circumstance that all of the Irgafos 168 degraded to this one degradate. A more reasonable example, might be the case where 10% of the Irgafos 168 degrades to firm this degradate, making the degradate's total pool 300 μg/g. In this case, use of eq 3 results in an estimated solution concentration of 0.65 mg/L for the degradate. Thus the more polar degradate will accumulate in solution to much higher levels than the poorly soluble parent compound, even though the degradate's pool is an order of magnitude less than that of the parent.
Additional examples of the utilization of partition coefficients to facilitate extractables and leachables assessments have been documented by Castner and associates (8, 9).
Factors Affecting Partitioning
The partitioning of solutes between dissimilar phases (and thus the accumulation of leachables in pharmaceutical solutions) will depend on the nature of the plastic, the nature of the solute and the nature of the solution. Considering the plastic, each plastic material will have its own unique interaction model (e.g., eq 5), although it can be anticipated and has been demonstrated that interaction models for similar materials (e.g., polypropylenes as a material class) are themselves similar. It is clear from eq 3 that the material's weight and the solution's volume (and especially the ratio of the two) have a considerable effect on a leachable's partition-mediated, equilibrium concentration in solution.
If a solute is ionizable, its Eb value will depend on the solute's dissociation constant (pKa or pKb as appropriate) and the solution's pH in the same way that these properties effect, for example, an apparent partition coefficient (known as the distribution coefficient). If the leachable is a weak organic acid (HA), it will be in its prontonated form (HA) if the solution pH is below the acid's pKa. If the solution pH is above the acid's pKa, the organic acid will exist in it dissociated form (A−). Because the aqueous solubility of the dissociated form is much greater than that of the prontonated form, the concentration of acid leached from a plastic and into an aqueous solution will be greater at the higher pH. Alternately, the concentration of neutral leachables will be largely unaffected by solution pH.
This effect of solution pH on the partitioning of an ionic solute can be expressed mathematically as follows:
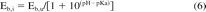
where Eb,i is the interaction constant at a particular pH and Eb,u is the interaction constant of the undissociated form of the acid. This impact of this effect can be illustrated as follows. Consider a weak acid leachable with a pKa of 5.5 and an Eb,u of 100 (more or less consistent with fatty acids such as stearic acid, a common material additive or processing aid). At pH 4.0, the value of Eb,i is calculated as 97, while at pH 8.0 the calculated value of Eb,i is 0.32. As the concentration of the leachable acid is roughly inversely proportional to Eb, this difference of 4 pH unit results in approximately a 300-fold difference in the leachable's solution concentration. As a general rule of thumb, the maximum solution concentration of an acidic leachable will be observed at a pH that is 2 units above the acid's pKa, while the minimum solution concentration of an acidic leachable will be observed at a pH that is 2 units below the pKa.
The impact of solution pH on the accumulation of leachables has been experimentally verified. For example, the accumulation of 2-ethylhexanoic acid (pKa = 4.85) leached from a styrene-butadiene-styrene block co-polymer was reported to increase from 2.62 to 5.44 ppm as solution pH increased from 2.3 to 6.0 (3). The accumulation of fatty acids (such as myristic, palmitc and stearic acids, with pKa in the range of 5 to 6) leached from an irradiated ethylenevinyl acetate polymer has been reported to be markedly increased as solution pH increases past pH 8 (10). While the leaching of acidic compounds from a polyolefin material was strongly influenced by pH over the range of 3 to 7, the leaching of neutral compounds was largely unaffected by pH (see Table I) (2).
Accumulation Levels of Compounds Leached from a Polyolefin Material (1)
Similarly, the impact of solution pH on the leaching of stearate and stearic acid salts from plastic materials has been investigated (11). At low pH, the cation counterions of the stearate salts are extracted from the plastic materials by a process that can loosely be termed ion exchange. At intermediate pH, little or no extraction of the stearates occurs. At high pH, the stearates are extracted from the materials to a limited extent due to the solubility of the acid and/or salts in the extraction medium. It is noted that for plastic materials that contain both stearic acid and a source of a precipitating cation (e.g., zinc oxide), the formation of particulate matter during the extraction is possible.
Because pharmaceutical solutions can be compositionally complex, compositional factors other than pH could affect partitioning. For example, pharmaceutical solutions may contain relatively high concentrations of salts (e.g., buffers, osmotic and tonicity agents), sugars (e.g., dextrose) and other ionic and non-ionic ingredients. It is well established that the presence of such entities in solutions can affect the partitioning phenomenon. For example, addition of relatively large quantities of an inorganic salt (such as NaCl) to an aqueous test sample is known to facilitate the extraction of that sample with an organic solvent (e.g., the “salting out” effect). In the case of leachables, the effect would be one of “salting in”; that is, the presence of salts and other solution components would reduce the ability of leachables to migrate out of the plastic and into the solution. Alternatively, increasing the ionic strength of the pharmaceutical solution could increase the migration of inorganics and/or metal-containing additives and catalysts via ion pair formation.
This impact of solution composition was addressed in a study in which interaction constants between a polyolefin material and numerous model compounds were measured in a number of representative parenteral products/diluents, including saline, dextrose, mixed salt, and amino acid solutions (12). For the non-ionic model compounds, the interaction constants were not appreciably affected by the different solution compositions, while for the ionic model compounds, the effect of solution composition on the interaction constants could be directly attributed to solution pH. These experimental results suggest that the presence of “inactive” formulation components in many pharmaceutical solutions will not appreciably affect the partitioning phenomenon and, by extension, the accumulation of leachables in such solutions.
More recently, the effect of extracting phase composition on the extraction of substances from rubber stoppers was reported (13). The findings reported by these authors were as follows:
Formulation pH plays a minor role in the levels of extractables. The effect of pH observed by these authors is a result of their experimental design, as the pH range studied was small (5.0–8.2) and the extractables considered were neither acidic nor basic.
The presence of excipients imparts a variable effect of the accumulation of extractables. While the authors note that the solubilizer Tween 80 has a significant effect, increasing the levels of extractables, a chelating agent (ethylenediaminetetraacetic acid, EDTA) had no effect on neutral extractable and bulking agents (such as sucrose, mannitol, and trehalose) had a minimal impact.
The formulation of poorly soluble drugs with solubilizing agents is becoming more common in pharmaceutical product development. Inclusion of such agents in a pharmaceutical solution would logically have a marked effect on the plastic/solution partitioning phenomenon and thus on the accumulation of leachables in the drug product. It stands to reason that an agent that increases the solubility of a drug in a product would also increase the solubility of a leachable in that product. An example of this phenomenon is the documented incompatibility of bis(2-ethylhexyl)phthalate (DEHP)-plasticized polyvinyl chloride (PVC) containers with drug products formulated with such solubilizing agents (14–18). With a Po/w > 108, DEHP will accumulate in water-like drug products at relatively low levels (much less than 1 mg/L), even though this compound is present in plasticized PVC materials in amounts on the order of 20 to 40 weight percent. However, much higher concentrations of leached DEHP are reported in drug solution vehicles that contain solubilizing agents.
The increased ability of a drug product containing solubilizing agents to leach substances from plastics can be at least partially attributed to the agent's ability to influence the apparent polarity of the drug product. That is, the net effect of the solubilizing agent is to reduce the apparent polarity of an aqueous formulation, rendering the aqueous product less polar (and more non-polar) and thus more hospitable for the generally non-polar leachables. In the practical sense, the change in polarity of the solution phase causes a decrease in the interaction constant and a corresponding increase in the leachable's accumulation levels.
Understanding the impact of pharmaceutical solubilizing agents on leachables accumulation is important for two reasons. Firstly, it would be useful to be able to predict the effect that a solubilizing agent would have on the accumulation of non-polar leachables, for example, in the same way one can predict the effect that solution pH will have on the accumulation of ionic leachables. Secondly, performing extractables assessments (and even targeted leachables assessments) in pharmaceutical solutions containing these solubilizing agents is a difficult analytical challenge that could be simplified greatly if such assessments could be performed with a more analytically expedient surrogate or model solvent system. Choosing and justifying such a surrogate solvent system requires that one is able to quantify the solubilizing agent's effect on the partitioning phenomenon.
Understanding and quantifying the impact that various solubilizing agents have on leachables accumulation is a two-step process. In the first step, a relationship between a solution's polarity and the accumulation of leachables must be uncovered and delineated. In the second step, such a relationship must be extended to include a consideration of the solubilizing agent's ability to affect the polarity of a pharmaceutical solution. The first step can be accomplished using solvent systems of known composition and polarity. If one examined the plastic/solution partitioning of solutes in solvent systems of different polarities (as could be achieved, for example, with systems containing different proportions of an organic solvent like ethanol), one could, in principle, establish a relationship between polarity and the interaction constant. The same outcome could be achieved if one measured the accumulation of leachables in solvent systems of different polarities.
Studies that accomplish these objectives and designs have been reported in the literature (2, 6, 10, 19) and generally suggest that an empirical relationship can be established between Eb and the polarity (P) of the solvent phase:

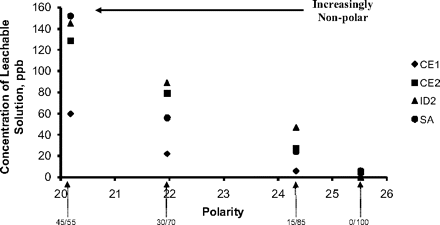
where the coefficients a and b can be empirically derived and are dependent on the specific leachable. Such a relationship is shown in Figure 2, which documents the accumulation levels of several compounds leached from a polyolefin laminate by solutions of varying ethanol/water proportion (and thus polarity). As one would expect, as the polarity of the solution decreases (becoming more non-polar), so too does the concentration of relatively non-polar leached substances.
Effect of solvent polarity on the accumulation level of several leachbles. The accumulation levels of the leachables (CE1 = 5578-82-5, CE2 = 94113-50-5, ID2 = 20170-32-5, SA = 57-11-4) are inversely proportional to the stored solution's polarity for binary ethanol/water systems. As the solution becomes more polar, the concentration of the leachable increases, with the magnitude of the increase being greater for the more non-polar leachables. The number that appears by the arrows is the proportion of ethanol and water in the binary solutions. The polarity of the solvent is expressed as the Hildebrand solubility parameter δ, which has a value of 25.52 cal1/2cm−3/2 for water and 13.65 for ethanol. Abstracted from Reference 6.
The second step in terms of understanding and quantifying the impact that various solubilizing agents have on leachables accumulation is establishing the agent's intrinsic polarity. Unlike a pure solvent, whose polarity is known (or can be readily documented), the polarities of these agents are either unknown and or undocumented and thus must be determined experimentally. One means that was used to accomplish this objective is to prepare test mixtures of compounds with known partition coefficients in solvent/water systems (including various binary mixtures of ethanol/water, acetonitrile/water) and various solubilizing agents commonly encountered in pharmaceutical formulations (e.g., Tween 80, Lecithin, Chemophor EL, sodium dodecylsulfate [SDS]) (18). These donor solutions were contacted with a polyolefin material until equilibrium was achieved and the equilibrium concentration of the compound remaining in solution was measured. One recognizes that while such a binding study is the reverse of a leaching study (that is, the compound migrates into the plastic and not out of the plastic), the binding and leaching phenomena are essentially mirror images of the same physicochemical process. The resulting information is used to calculate interaction constants for the model compounds in all the test solutions. A comparison of the interaction constants across the various solution types allows the solutions to be contrasted in terms of their apparent polarity.
The results of such an investigation were as follows. Solutions containing 5% Tween 80 and 0.2% SDS were well-behaved in the sense that the compound partitioning in these solutions fit the previously described model and thus that their “polarities” could be determined. Specifically, the 5% Tween 80 solution was effectively modeled by an approximately 25/75 ethanol/water mixture. Similarly, the SDS solution was effectively modeled by a 5/95 ethanol/water mixture. The other two solubilizing agents studied, 25% Cremophor EL and 1% Lechithin, were not well-behaved in the sense that the partitioning behavior of compounds in these solutions did not fit the previously described model. This suggests that these agents perform their solubilization function via mechanisms that are not solely polarity-driven.
The use of thermodynamic principles to facilitate extractables and/or leachables testing can be illustrated via the following situation. Discovering, identifying, and quantifying extractables are the critical aspects of the extractables profiling process. It is generally recognized that the higher the concentration of extractables in the extract, the more likely it is that these activities will succeed. Thus, extraction conditions are frequently designed to increase the concentration of one or more extractables. One means used to accomplish this objective is to extract a greater amount of plastic. While such an approach may make intuitive sense, it may not be consistent with the thermodynamic constraints inherent in the extraction process.
It is relatively straightforward to understand that increasing the amount of material extracted will not increase the amount of extractable in an extract if the extractable is already present in the extract at its solubility limit. Less easy to understand but similarly true is the observation that partitioning will limit the magnitude of any increase in extractables concentration in the extract derived by increasing the amount of material extracted. This situation can be illustrated by the following example. A plastic material contains 1000 μg/g (ppm) of an additive. The volume of extracting solution is 100 mL. If the amount of material extracted increases from 10 g to 100 g, how much will the extractable's concentration in the extract change? Because the answer will vary depending on the extractable's interaction constant (Eb), four scenarios are considered: Eb = 0 (extractable is fully soluble in the extracting medium) to Eb = 100 (extractable partitions strongly into the plastic).
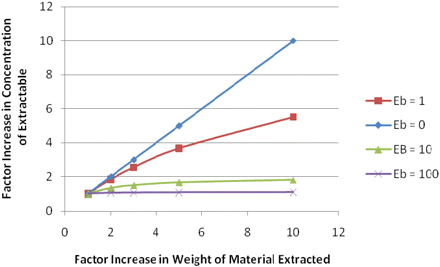
The outcome of such an assessment is illustrated in Figure 3. For an extractable with an equilibrium interaction constant (Eb) of 0 (extractable has no affinity for the plastic), an increase in the amount extracted results in a directly proportional increase in the extractable's concentration (for example, increasing the amount of material extracted by a factor of 10 increases the extractable's concentration by the same factor). However, as the extractable's affinity for the plastic increases, for example, if the extractable becomes more non-polar and Eb increases, the increase in extractable's concentration derived by increasing the amount of material extracted is reduced. For example, an extractable with an Eb value of 1 will see its concentration in the extract increase by a factor of roughly 5 for every 10-fold increase in amount of material extracted. At an Eb value of 10, increasing the amount of material extracted by a factor of 10 will less than double the extractable's concentration in the extract. In such a circumstance, increasing the mass extracted would not produce a large enough increase in the extractable's concentration to materially improve the performance of the analytical process (compound discovery, identification, and quantitation).
Effect of increasing the amount of material extracted on the concentration of an extractable in the extract. For an extractable with an equilibrium interaction constant (Eb) of 0 (no affinity for the plastic), an increase in the amount extracted results in a directly proportional increase in the extractable's concentration. However, as the extractable's affinity for the plastic increases (e.g., the extractable becomes more plastic-like and Eb increases), the increase in extractable's concentration derived by increasing the amount of material extracted is reduced. In extreme cases, increasing the amount of material extracted will not increase the extractable's solution concentration (as is the case for Eb = 100).
Kinetics of Migration
General
A thermodynamic assessment of a material/solution interaction establishes the maximal, worst-case, equilibrium-driven accumulation of a leachable in a solution product. The kinetic assessment of a material/solution interaction considers the possibility that equilibrium is not achieved under the conditions of contact or that there are factors, such as the decomposition of the leachable, which perturbs the equilibrium state. In either case, the net result of a kinetic assessment is a leachables accumulation that is less than that obtained via a thermodynamic assessment.
Migration/Diffusion
In some pharmaceutical applications, the nature of the plastic/solution interaction is such that equilibrium is achieved and thus the accumulation of leachables can be estimated using the thermodynamic models discussed previously. An example of such a system would be a drug formulation that is filled into a packaging system, terminally sterilized (autoclaved) and stored (packaged) for extended periods of time. Such rigorous contact conditions would drive the solution–material system to equilibrium. In other cases, the conditions of contact are insufficiently rigorous for equilibrium to be achieved; examples are a pharmaceutical intermediate being filtered to produce a final drug product, a drug being admixed into a large volume parenteral LVP diluent (in a plastic bag) and then used within the relatively short shelf life of the admixture, and an aseptically filled packaging system (e.g., pre-filled syringe). Under non-equilibrium contact conditions, the leachable's migration, or diffusion, rate through the plastic material will ultimately establish the leachable's concentration in the contacted solution.
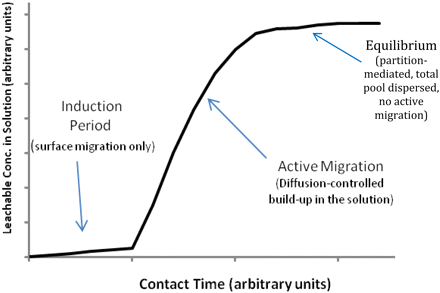
The migration (diffusion) of compounds through plastics has been extensively investigated, as this topic is important to industries other than pharmaceuticals (e.g., the food industry) and in applications other than packaging (e.g., drug delivery). It is beyond the scope of this article to either detail the extensive literature or delineate the numerous mathematical models that exist on the general topic of migration of compounds through (and out of) polymers; however, examples of studies relevant to parenteral packaging can be found in References (20 and 21). In Reference (20), for example, a three stage migration model is proposed for the migration of a leachable from a container and into its contained solution (Figure 4). Stage 1 of the model is the induction period (allowing for the leachable to migrate through the plastic to the container's surface), during which little if any leachable migrates into the solution. The small amount of the leachable that accumulates in solution during the induction period is typically that amount of the leachables that is present on the surface of the material's solution-contact surface. The induction period is followed by an active period of leaching, where the leachable's diffusion-mediated concentration in solution can be determined using the following relationship:
A three compartment migration model for the leaching of a Compound from a Plastic Container and Into a Contained Solution (from Reference 20). An induction period, characterized by little or no migration of the leachable into solution, is followed by a active period of diffusion mediated migration of the leachable into solution. The induction period essentially represents release of the leachables that are on the surface of the material at the initiation of the contact. The diffusion period represent the release of leachables that have migrated through the material to reach the contact surface. Eventually, the leachable accumulates in solution to its maximal, equilibrium-driven concentration and the migration (diffusion) process stops.

where D is the diffusion coefficient, t is time, δ is the thickness of the container material, Mt is the amount of the leachable that has leached into the solution at time t, and M∞ is the amount of the leachable that is leached into solution at equilibrium (presumably obtained at infinite contact time). Eventually, the system (defined by the container and its contained solution) reaches equilibrium and the leaching stops, resulting in a partition-mediated leachable level in the solution.
It is appropriate to note that this extensive body of knowledge has established that migration of compounds from contact materials into contacted entities is a predictable physical process readily amenable to mathematically modeling. In fact, within the food industry the utilization of “generally recognized diffusion models” to “verify compliance with specific migration limits” is a well-accepted practice in both the US (22) and European (23) regulatory communities. It remains to be seen whether such a situation can be achieved in all or selected parts of the pharmaceutical industry. Certainly an important factor that limits the general pharmaceutical application of such models is the great complexity and diversity of pharmaceutical products and the systems or materials that they contact.
System parameters that affect the migration process include the following:
Properties of the migrating entity (i.e., leachable): interaction constant, diffusion coefficient,
Properties of the contact material: interaction constant, diffusion coefficient, total pool of migrant, homogeneity and/or structure (such as layering), distribution of the migrant within the material, thickness, physical or chemical treatment (e.g., irradiation), and
Conditions of contact: duration, temperature, contact surface area, nature of contact (e.g., direct, indirect, remote)
While it is beyond the scope of this article to provide a comprehensive review of the mathematics involved in considering the impact that these parameters have, either individually or in aggregate, on the levels to which leachables will accumulate in a drug product, useful and appropriate mathematical models exist and can be used to estimate leachable accumulations under many simple and straightforward contact scenarios.
Post-Migration Degradation of the Leachable
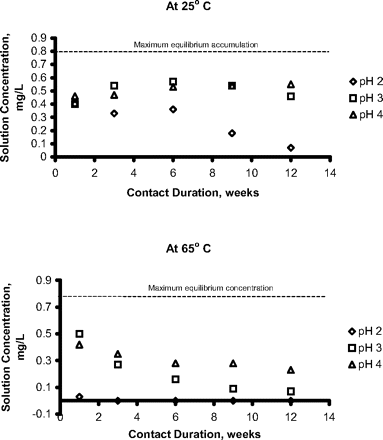
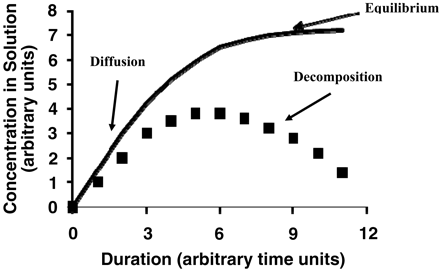
The worst-case accumulation of a leachable (greatest accumulation level) will occur if a leachable is chemically stable in the solution into which it migrates. If this is not the case, a leachable's concentration in a drug product will be influenced by its decomposition rate. For example, it has been shown that certain carboxylic acid alkyl esters are leachables associated with laminated polyolefin films (24). These alkyl esters undergo acid- and base-catalyzed hydrolysis in aqueous solutions and thus their accumulation in solution depends on contact conditions (duration and temperature) and solution pH—for example, Figure 5. In such a case, the relationship between the leachable's concentration in solution and the duration of the contact will depend on the juxtaposition of the migration rate and the decomposition rate. If the migration rate is fast and the decomposition rate is slow, then the leachable's accumulation will approach its partition-mediated equilibrium value. On the other hand, if the migration rate is slow and the decomposition rate is high, then the leachables' accumulation in solution will be minimal. An example of the accumulation profile that could be observed in such a case is illustrated in Figure 6.
Accumulation of a leachable that degrades in the contacted solution. The leachable undergoes acid catalyzed degradation and thus its accumulation reflects the juxtaposition of migration and degradation rates. The different accumulation profiles at 25 °C and 65 °C reflect the difference in temperature-dependence of the diffusion coefficient and the degradation rate constant. Data abstracted from Reference 24.
Idealized accumulation profile of a leachable that undergoes decomposition in the drug product. During the early stage of contact between the plastic and the drug product, the leachable will accumulate in a manner that is kinetically constrained by its migration (diffusion) rate in the plastic. If the leachable were stable in the drug product, its accumulation would eventually reach the thermodynamically constrained equilibrium maximum concentration. The solid line represents the accumulation profile in the absence of degradation. Because the leachable degrades, its actual accumulation profile (denoted by the squares) diverges from the thermodynamic model. As the leachable's accumulation level increases, so too does its decomposition rate. At some point, the decomposition rate exceeds the migration rate and the leachable's concentration will decrease. If the contact duration is sufficiently long, the total pool of the leachable in the plastic will eventually be depleted, the leachable will completely degrade and its solution concentration will approach zero.
Should the primary leachable degrade in the solution into which it migrates, the degradation product becomes a secondary leachable. The accumulation profile of this secondary leachable in the drug product will mirror the accumulation profile of the primary leachable.
Concluding Comments
Extractables and leachables assessments performed in accord with existing regulatory guidance require rigorous testing of plastics and drug products (and associated solutions) that the plastic contact. Although mathematical modeling is accepted as a standard approach in the food industry, modeling of extractables and leachables behavior in pharmaceutical products is not generally recognized as an acceptable assessment approach in the various regulatory guidance and guideline documents. Nevertheless, a firm understanding of the fundamental physiochemical process that control and influence the interaction between a plastic material and a drug product can greatly facilitate the design, implementation, and interpretation of extractables and leachables assessments.
Conflict of Interest Declaration
The author declares that he has no competing interests.
- ©PDA, Inc. 2011