Abstract
New recommendations for the validation of rapid microbiological methods have been included in the revised Technical Report 33 release from the PDA. The changes include a more comprehensive review of the statistical methods to be used to analyze data obtained during validation. This case study applies those statistical methods to accuracy, precision, ruggedness, and equivalence data obtained using a rapid microbiological methods system being evaluated for water bioburden testing. Results presented demonstrate that the statistical methods described in the PDA Technical Report 33 chapter can all be successfully applied to the rapid microbiological method data sets and gave the same interpretation for equivalence to the standard method. The rapid microbiological method was in general able to pass the requirements of PDA Technical Report 33, though the study shows that there can be occasional outlying results and that caution should be used when applying statistical methods to low average colony-forming unit values.
LAY ABSTRACT: Prior to use in a quality-controlled environment, any new method or technology has to be shown to work as designed by the manufacturer for the purpose required. For new rapid microbiological methods that detect and enumerate contaminating microorganisms, additional recommendations have been provided in the revised PDA Technical Report No. 33. The changes include a more comprehensive review of the statistical methods to be used to analyze data obtained during validation. This paper applies those statistical methods to analyze accuracy, precision, ruggedness, and equivalence data obtained using a rapid microbiological method system being validated for water bioburden testing. The case study demonstrates that the statistical methods described in the PDA Technical Report No. 33 chapter can be successfully applied to rapid microbiological method data sets and give the same comparability results for similarity or difference as the standard method.
Introduction
PDA Technical Report 33 (TR33)—Evaluation, Validation and Implementation of Alternative and Rapid Microbiological Methods (1) has recently been comprehensively revised to account for the many changes that have occurred since its initial release in 2000. A key improvement is the fuller description of the statistical methods that the user of new methods can apply to analyze the data generated during the method validation. However, the TR33 document does not contain any detailed examples of the statistical tests with the actual data to demonstrate their practical application.
To test the general application of the statistical tests suggested in TR33, results obtained during an evaluation of the Growth Direct™ (GD) System are shown. The GD technology can be defined an automated rapid microbial method, as it is based on the traditional compendia plate count (PC) test, but with the incubation and colony enumeration steps fully automated. The approach taken for the evaluation of the GD System was as defined in section 3.7 Automated Methods in TR33 and followed the methods and acceptance criteria of section 5. Growing microscopic colonies are detected by the GD System through the increase in their inherent auto-fluorescence, which the system records over time. The GD System differentiates inanimate fluorescent debris (false positives) from growing micro-colonies, as the former do not change in intensity, shape, or size with incubation.
A method validation procedure may be thought of as a designed experiment to evaluate any of the ten specific criteria as listed in Table 5.3-1 of TR33. This paper illustrates the design and statistical analyses for two cases:
An intra-laboratory study conducted involving multiple operators using prepared suspensions of six microorganisms to evaluate the precision, ruggedness, and accuracy of the two test methods (GD and PC), and to assess the equivalence of the GD method with respect to the PC method.
A paired comparison study conducted on bioburden in purified water samples taken over multiple time periods at four sampling points to evaluate the equivalence of the GD method with respect to the PC method.
The statistical analysis was conducted using the Minitab® 16.2.4 statistical computer package and spreadsheet calculations using Microsoft Excel®.
Intra-laboratory Study
Objective
This study was designed to
Estimate and compare the repeatability and intermediate precision of the two test methods (Sections 5.3.2 and 5.3.8 of TR33).
Evaluate the accuracy and equivalence of the GD method against the PC method (Sections 5.3.1 and 5.3.10 of TR33).
Methods and Materials
Four trained operators in the laboratory participated in the evaluation using individual calibrated, automated pipettes. Four operators were used in order to look at the operator-to-operator variation. Six organisms used in the study were obtained as Quanti-Cult+ ® commercial preparations from Remel (Lenexa, KS, USA) and recommended in the U.S. Pharmacopeia (USP). The species tested were
Pseudomonas aeruginosa ATCC #9027.
Candida albicans ATTC #10231.
Bacillus subtilis ATCC #6633.
Aspergillus brasiliensis ATCC #16404.
Staphylococcus aureus ATCC #6538.
Escherichia coli ATCC #8739.
Each microorganism suspension was prepared to give 10–100 colony-forming units (CFU) per inoculum (100 μL) in a sufficient volume to perform all four operators' tests at the same time. The spiking of 100 μL to 20 mL of Fluid A was performed for each microorganism at the same time by the operators to minimize any changes in the bacterial numbers. The samples were filtered using either the GD Filtration Kit or MicroFil-V (EMD-Millipore, Billerica, MA) funnels, and six membranes were transferred to the R2A media surface for each of the GD method and the control PC methods.
The control PC method followed the guidelines in the European Pharmacopeia with incubation on R2A at 30–35 °C for at least 5 days. The growth cassettes were transferred to the GD System and incubated at the required temperature of 30–35 °C for 5 days (120 h). At the end of the incubation all tests were removed and the colony counts enumerated by three independent operators for each plate/cassette. The use of three operators to enumerate the colonies sought to minimize any operator-to-operator variation for the accurate enumeration of the visual CFU.
Experimental Design and Statistical Analysis
The six microbial species were evaluated using an identical experimental design. This involved the use of a completely randomized design with a single response (CFU count) and two factors (input variables) as follows:
Test Method (two levels)—Growth Direct (GD) and compendia plate count (PC).
Operator (four levels)—identified as Operators 1, 2, 3, and 4.
Twelve aliquots of each microorganism suspension sampled by each operator were treated as indistinguishable experimental units. Six of these aliquots were randomly assigned to each of the two test methods, hence they were “completely randomized”. The resulting six replicate counts from each operator/method were considered to be independent test results conducted under repeatability conditions.
For evaluation of precision, the test results were separated by test method, and the precision of each test method was evaluated separately. Because of multiple operators in the design, the intermediate precision (ruggedness) was to be estimated as well as the repeatability. Precision is usually stated as a standard deviation or coefficient of variation (CV), also termed the relative standard deviation (RSD).
For evaluation of accuracy and equivalency, the entire design was utilized. The statistical analysis compared the mean responses from the two test methods allowing for variation among operators. Accuracy is often stated as the percent recovery of microorganisms of the alternative method relative to the compendia method. Equivalence is stated as the agreement of mean test results with respect to a predefined limit.
Data and Preliminary Statistics
The test results are listed in Table I by method, operator, and replicate with a separate column for each microorganism. The GD test results were integer counts determined automatically by the system apparatus, and the PC test results were the averages of independent plate counts by three readers, rounded to one decimal place.
Accuracy and Precision Test Data
Table II lists the average, standard deviation, and CV by method, operator, and microorganism based on the six replicates. The averages ranged from 30 to 80 CFU depending on the microorganism, so a normal distribution model should apply for statistical testing. Within-operator standard deviations (n = 6) ranged from 3.1 to 13.4 CFU. Within-operator CVs ranged from 7% to 27%, thus comparing favorably with the expected value of 35% for a compendia test based on a Poisson distribution model (see TR33 Acceptance Criteria 5.3.2).
Summary Statistics by Method, Operator, and Microorganism (n = 6)
Precision and Ruggedness Results
Repeatability and intermediate precision were estimated independently by test method and microorganism. Table III summarizes the results of the statistical analysis for precision and ruggedness. For this experiment, ruggedness was interpreted as the intermediate precision, a type of intra-laboratory precision involving the effect of different operators on the test result variability as well as repeatability.
Results for Repeatability and Intermediate Precision
For the precision estimation, the four operators were treated as a random selection from a larger hypothetical population of operators. An analysis of variance (ANOVA) was the statistical method used to divide the total variation of each test method into two variance components: between-operator variance and within-operator variance. The latter variance is termed the repeatability variance of the test method.
The operator variance was an indirect estimate using the variance of the operator averages along with the repeatability variance to estimate the variance component due to operator differences. A negative estimate of this component was possible if the operator agreement was very good; if so, the between-operator variance component was set to zero. The intermediate precision variance was the sum of the within-operator and between-operator variances. The statistical calculations are shown in greater detail in the Precision section of the Appendix.
The variance estimates for each test method are listed under “Variance Components” in Table III as well as the percent contribution of between-operator variance to the total variance. The repeatability variance for the GD method was numerically lower than the PC method except for E. coli. Also, the intermediate precision variance for the GD method was numerically lower except for A. brasiliensis and E. coli. The operator contribution to total variance was higher in the GD method for A. brasiliensis and in the PC method for S. aureus, so that these two cases demonstrated less ruggedness than the rest of the cases.
Note that the operator variance estimates of the GD method were zero for four of the six microorganisms, indicating negligible operator influence and thus good ruggedness for the GD method in these cases.
Precision estimates are usually stated as a standard deviation or a coefficient of variation (CV), and these are listed for repeatability and intermediate precision of both methods under “Precision Estimates” in Table III. All repeatability CVs were well below the benchmark 35%, with the maximum CV at 19%.
The Poisson distribution is generally used to model the variation in plate count due to sampling from a suspension and has the property that the ratio of the variance to the mean is equal to unity (1). This ratio fluctuated around unity for the GD method but was above unity for the PC method, the exception being the E. coli results. This would indicate some extra Poisson variation due to other sources of variation in the PC test method, whereas the GD method variation was mainly due to sampling variation.
An F-test was used to compare the repeatability variances of both test methods in Table III. No significant difference in repeatability precision between test methods was found for any of the six microorganisms. The P-values were calculated by means of the F distribution (FDIST) function in Excel using the variance ratio and the degrees of freedom for each variance as entries for the FDIST function.
Accuracy and Equivalence Results
The full design (data from both test methods) was used for evaluating accuracy and equivalence for each microorganism. A fixed effects model was used in an ANOVA to evaluate accuracy, treating method and operator as fixed factors and also including the method by operator interaction as a fixed factor. The interaction effect measures the difference of the operator effect between the test methods. The error variance in the model equals the repeatability variance. This model interpreted the operators as fixed members of the current staff utilized for this test rather than as being randomly selected from a larger population of operators and allowed the evaluation of these specific operators. The statistical calculations are shown in greater detail in the Accuracy section of the Appendix.
The results of the statistical analyses for accuracy are summarized under the “Accuracy” section of Table IV. The test result averages (n = 24) are again listed in Table IV for each test method on the six microorganisms, and the difference between methods ranged from −5% to 6% relative to the PC method. An ANOVA was conducted on the full data set for each microorganism, and the P-values for method, operator, and method × operator interaction effects are listed. All P-values for method were above the 0.05 significance level, indicating no statistically significant difference between test methods for any of the six microorganisms. This result would support the accuracy of the GD method with respect to the compendia PC method.
Results for Accuracy and Equivalence
Statistically significant operator differences were found for S. aureus and A. brasiliensis, and this could be explained by the larger operator effect for the GD method for these two microorganisms, as noted earlier. The statistically significant method by operator interaction seen for A. brasiliensis was due to Operator 3 having much higher GD test results than the other operators but also having similar PC test results. The variation in operator counts seen here may be related to the difficulty in obtaining a consistent homogenous sample preparation. Some organisms are prone to clumping in suspension and can dissociate under filtration to give higher CFU counts.
The normality assumption for the CFU data was tested by the Anderson-Darling (AD) (5) procedure on the residuals from the fixed model analysis of variance. The residuals were the deviations of the test results from their average in each group of six test results, and these were collected over the eight combinations of test methods and operators, with 48 residuals for each microorganism. The AD null hypothesis is that the data are normally distributed, and a low P-value refutes this hypothesis. The AD P-values listed in Table lV were well above the 0.05 significance level, so the normality assumption was supported for all microorganisms in this experiment. A logarithmic transformation was not necessary, as each set of data were in less than an order of magnitude in range. However, a logarithmic transformation is necessary when the test results vary over two or more orders of magnitude.
Equivalence testing was conducted from the standpoint of non-inferiority of the candidate test method against the compendia method. For detection of viable microorganisms, non-inferiority is defined as the candidate method CFU count being no less than 70% of the compendia method count at 95% confidence. (On a log scale this would be approximately no less than a 0.5 log difference).
A statistical test for non-inferiority used the single one-sided t-test on mean test results from each method. The key result is the lower one-sided 95% confidence limit on the mean difference (GD minus PC) relative to the PC mean. Because the PC means vary from case to case, a normalized test statistic was used equal to
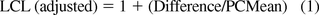having an acceptance criterion of not less than 0.7. A summary of the one-sided t-test methodology is given in the Appendix.
Two sets of statistical tests were conducted on each microorganism, one set using all of the data, and another set by results from each of the four individual operators. The results for the non-inferiority tests are listed under the “Equivalence” section in Table IV.
The statistical tests based on the complete data set for all six microorganisms easily passed the non-inferiority test with adjusted lower confidence level (LCL) results ranging 0.82 to 0.96, well above the 0.7 acceptance criterion. These were examples of testing conducted under intermediate precision conditions where operator differences were taken into account.
The 24 statistical tests by individual operator all passed except for Operator 4 testing A. brasiliensis, with an adjusted LCL value of 0.69. Five cases fell in the 0.70–0.75 range, indicating that n = 6 replicates might have resulted in an underpowered statistical test. These cases were examples of testing conducted under repeatability conditions, where better precision was traded off against a larger-sized set of data made available by combining the operator data.
Paired Comparison Study
Objective
This study was designed to evaluate the accuracy and equivalency of the GD method against the PC method on actual water samples from a working environment (Sections 5.3.1 and 5.3.10 of TR33).
Method
Water samples were taken from four sample points around the water purification system to represent different bioburden levels. Sample Point 1 was at the water for injection loop, Sampling Points 2 and 3 were purified water taken from drops near the reverse osmosis process, and Sampling Point 4 was taken after the water softening stage. Water samples were collected over 20 days at each of the four sampling points. Each water sample was then split into two aliquots: 1 mL each at Sampling Point 4 and 200 mL each for Sampling Points 1, 2, and 3. The aliquots were then filtered singly on either the company's Micro Fil-V filtration method or the GD Filtration Kit.
Experimental Design and Statistical Analysis
This was a randomized block design with a single response (CFU count) and two factors (input variables) as follows:
Test method (two levels)—Growth Direct (GD) and compendia plate count (PC).
Sampling time (20 levels) indicated by a sequential number.
The sampling time was a nuisance factor, or block, that accounted for the fact that the true CFU varied over time. Each block, or sampling time, consisted of two water sub-samples which were each randomly assigned to a test method, hence the term randomized block. For the current situation with only two levels of the test method factor of interest, this design is also known as a paired samples design, because single GD and PC test results were paired in each block, designated by time of sample.
The data analysis of a randomized block design generally utilizes the two-way ANOVA, which gives P-values for the statistical significance of test method and blocks, and the block-by-method interaction is the error term.
In the present cases, where the test method factor has only two levels, GD and PC, a Student's t test on the test result differences between the two methods will give the P-value for the statistical significance of the method effect. The two-sided confidence interval may be used to test for a mean difference deviating from zero by inclusion of zero within the confidence interval indicating no significant difference and non-inclusion indicating a statistically significant difference. The computer output from Minitab is discussed in the Appendix.
Accuracy and Equivalence Results
The CFU data are listed in Table V for the two processes. Single test results by the traditional P) method and the GD method are listed for each sampling time with average maximum and minimum values over all sampling times. Also listed are the calculated differences (GD minus PC) for each sample. A positive difference indicated higher sensitivity in detection for the GD method. The CFU ranges varied by sampling point.
Pharmaceutical Water System CFU Data from Four Sampling Locations Sampled on 20 Separate Occasions
Sampling Point 1:
For the 20 sampling times at Sampling Point 1 all PC counts were zero and the GD count comprised four values of 1 CFU and 16 values of zero CFU. The data may be treated as binary outcomes if non-zero counts are classified as positives and zero counts as negatives. Then statistical tests for binary data may be applied, such as the McNemar test. However, much more data would be required (on the order of 50 to 200 paired observations) to perform a binary statistical test.
Sampling Point 2:
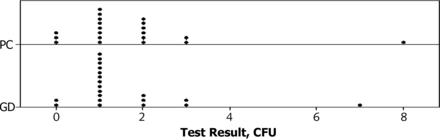
The test results at Sampling Point 2 were generally in the low count range of 0 to 3 CFU, with two higher excursions to 7 CFU for GD and 8 CFU for PC, occurring at different sampling times and for different test methods. The average results were in the Poisson distribution range of 0 to 15 CFU; therefore an equivalence test was conducted on the square root transformed data. The calculations are shown in Table Vl. The acceptance criterion for non-inferiority was that the lower 95% confidence limit (LCL) on the mean difference was greater than −30% of the PC average. For all 20 sampling periods the data did not support non-inferiority, as the LCL was −33.0%.
Equivalence Test Calculations for Sampling Points 2 & 3: Square Root–Transformed Count Data
A problem with the data set was the presence of the two high test results that increased the width of the confidence interval (see Figure 1). Although statistical testing would have identified the two test results as outliers, these results could not be rejected unless a physical cause could be found. It is likely that sampling contamination was involved because the high results occurred at different sampling times and for both test methods.
Dotplot of CFU counts by method.
Sampling Point 3:
At Sampling Point 3 the test results were in a higher count range of 0 to 20 CFU, and the average counts were in the Poisson distribution range. A square root transformation of the differences will achieve distribution normality required for the t test. The equivalence test calculations based on square root–transformed data are shown in Table Vl, and the data supported non-inferiority with an LCL of −15.1%.
Sampling Point 4:
The test results at Sampling Point 4 were in the range of 17 to 213 CFU, covering over one order of magnitude; therefore, a log transformation was indicated. Table Vll shows the equivalence test calculations, and the data supported non-inferiority with a 95% one-sided LCL of 3.0%. In fact, the data would support superiority as the LCL exceeded a zero percent difference.
Equivalence Test Calculations for Sampling Point 4: Log10-Transformed Count Data
Conclusions
A series of statistical analyses, as recommended by TR33, were conducted as a case study on CFU data from an experiment designed to compare the Growth Direct (GD) method and the plate count (PC) method to evaluate the accuracy, precision, and ruggedness, of the two methods.
The accuracy of the GD method was found to be acceptable for the six microorganisms tested, both by a simple 70% cutoff evaluation and by the more stringent non-inferiority test. The test methods were in general found to be indistinguishable with regard to precision, although there were differences over microorganisms. In any case, all the percent CV results were below the 35% acceptance criteria. There was also good intermediate precision with the exception of one operator with one organism, though this is more likely explained by the difficulties of working with A. brasiliensis rather than any inherent difference in the methods.
The analyses also showed good equivalence between the GD method and the Plate Count method for water samples with average counts above 5 CFU, though it should be noted that even at 5 CFU, 20 replicates may not always be enough to prove non-inferiority. However, for water samples with very low counts, passing the statistical analyses proved difficult. This is due to the limitations of the statistical methods when dealing with low averages and a limited number of replicates.
Using data generated during the evaluation of the performance qualification and method suitability studies for the GD System, the statistical methods suggested in the new TR 33 document were generally found to be applicable to the successful validation of the GD System, though care should be taken in applying the statistical methods when average CFU values are very low.
Conflict of Interest Declaration
Julie Schwedock, Kham Nguyen, Anna Mills, and David Jones are employed at Rapid Micro Biosystems and Thomas D Murphy is a consultant to that company. David Jones was a member of the PDA task Force responsible for the publication of TR33.
Appendix—Statistical Calculations
Precision
The repeatability and intermediate precision of a test method are calculated used the one-way analysis of variance (ANOVA) method, which is available in commercial statistical computer packages. The objective in this case study is to estimate two variance components, the within-operator variance (symbol σW2) and the between-operator variance (symbol σB2). These estimates are calculated from an ANOVA table, as illustrated herein using the Minitab output for the PC and GD test methods for B. subtilis. In this study there were k = 4 operators, and each operator conducted n = 6 test results.
The ANOVA first works with the sum of the n squared deviations (SS) of each operator's test results from the operator's average with n − 1 = 5 degrees of freedom (DF) for each operator's data set. These SS are summed over operators to give the Error SS in the ANOVA table with k (n − 1)= 20 DF. The next step is to calculate the SS of the operator averages from the grand average times n to give the Operator SS with k − 1 = 3 DF. Then the mean squares (which are variances) are calculated as MS=SS/DF for Operators and Error. The Total SS are the sums-of-squares of the entire data set. The DF, SS, and MS values are summarized in the Analysis of Variance table in the Minitab output example below.
The Error MS directly estimates the within-operator variance of the test method, σW2. The Operator MS estimates the quantity σW2 + ησB2, so the between-operator estimate of σB2 is calculated indirectly from (Operator MS – Error MS)/n. The Total variance, the sum of the Error and Operator variance components, estimates the intermediate precision variance σI2 = σW2 + σB2, the variance of a single test result in a lab with multiple operators.
Nested ANOVA: Bsubt versus Operator—PC Method
Analysis of Variance for Bsubt
Variance Components
The repeatability variance estimate sW2 is the Error MS = 76.7561. The operator variance component estimate sB2 is (118.6382 – 76.7561)/6 = 6.980, and the intermediate precision variance is the sum of the two variance components: sT2 = sW2 + sB2 = 76.756 + 6.980 = 83.736. The repeatability and intermediate precision standard deviations are the square roots of the respective variances and equal 8.761 CFU and 9.151 CFU, respectively.
Nested ANOVA: Bsubt versus Operator—GD Method
Analysis of Variance for Bsubt
Variance Components
The GD results illustrate the case of a negative estimate for the between-operator variance component. This occurs when the true operator contribution to test method variation approaches zero, which is a good outcome. The usual convention is to set a negative variance component estimate to zero, and the intermediate precision estimate becomes equal to the repeatability precision estimate 7.422 CFU.
Accuracy
The accuracy criterion refers to systematic differences due to test methods and operators. These two factors are evaluated as fixed factors in a two-way ANOVA procedure. The Total sum of squares (SS) are divided into subsets of sums of squares attributed to method, operator, the method*operator (Meth*Oper) interaction, and error. The Error method squared (MS) is the pooled repeatability variance estimated over test methods and operators. The remaining MSs are used to form the F statistics to test for statistical significance of the three fixed effects using the Error MS as the denominator. For the A. brasiliensis example shown below, the F statistic for operators is the ratio of the Oper MS to the Error MS, or 303.72/63.64 = 4.77, with a P-value of 0.006. A P-value for an F statistic less than 0.05 indicates a statistically significant effect. The Meth*Oper interaction was also statistically significant with a P-value of less than 0.001.
Analysis of Variance for Abras, using Adjusted SS for Tests
Grouping Information Using Tukey Method and 95.0% Confidence for Abras Means that do not share a letter are significantly different
Equivalence
In microbiology a test for non-inferiority is often applied for equivalence testing of test methods. A margin of the mean difference (candidate method mean minus compendia method mean) from zero to −30% of the compendia mean is allowed for improvements in speed or other benefits of the candidate method. Another rationale is that this margin is roughly equivalent to half of a log difference in the log metric [log10(0.3) = −0.522], which is not considered to be a practically significant difference.
A statistical test for non-inferiority is the one-sided t-test for two independent samples of data, available in commercial statistical packages. The test is often conducted by determining the lower one-sided 95% confidence interval on the mean difference and normalizing to the average compendia test result. The statistical test is derived as follows: Calculate the average and standard deviation of the test results for each method. Let D equal the difference of the two test method averages, D = X̄GD − X̄PC. Let sD be the standard error of the difference D calculated from the standard deviations of the test results with f degrees of freedom (DF). The lower one-sided 95% confidence limit LCL = D − t sD, where t is the 95th percentile of the Student's t distribution with f degrees of freedom.
The acceptance criterion for non-inferiority is that LCL ≥ −0.3 X̄PC, or it can also be stated as LCLadj = [1 + LCL/X−[PC] 0.7.
If the testing is conducted by a single operator under repeatability conditions, the data set will consist of n test results by each method, and these data will be entered into the program. For the case of k multiple operators, each conducting n test results under repeatability conditions, the operator averages for each test method will be entered into the program, and this will take into account the between-operator variation as well as the repeatability for each test. Two examples of Minitab output are listed below for P. aeruginosa: Operator 4, and All Operators.
Two-sample T for Pareu
Difference = mu (GD) − mu (PC).
Estimate for difference: −5.28.
95% lower bound for difference: −11.42.
T-Test of difference = 0 (vs >): T-value = −1.56 P-value = 0.925 DF = 10.
Both use Pooled StDev = 5.8628.
LCLadj = 1 + (−11.42/39.62) = 0.71 Pass (not part of Minitab output).
Two-sample T for Pareu
Difference = mu (GD) − mu (PC).
Estimate for difference: −1.92.
95% lower bound for difference: −6.91.
T-Test of difference = 0 (vs >): T-value = −0.75 P-value = 0.759 DF = 6.
Both use Pooled StDev = 3.6290.
LCLadj = 1 + (−6.91/38.63) = 0.82 Pass (not part of Minitab output).
Footnotes
Statistical Consulting, Morristown, NJ, USA.
- © PDA, Inc. 2015
