Abstract
Biological medicinal products inevitably contain residual DNA from host cells. Therefore, there is a theoretical possibility that cellular DNA in a medicinal product may cause oncogenic or infective events. Over the past decades, quantification of such risk has been the subject of intense scientific and regulatory interest. While several methods have been proposed in the literature, they are primarily concerned with point estimation of the oncogenic and infective risk. In this article, we propose a full Bayesian procedure to assess the safety risk. Safety risk is redefined as the posterior probability for the safety factor to be above an acceptable limit. The formulation of the problem in the Bayesian framework makes it possible to incorporate the uncertainties of key parameters into the safety risk assessment. It also allows for taking full use of prior knowledge of the risk associated with residual DNA and the understanding of DNA removal process. As a result, the method not only provides a more accurate estimation of oncogenicity or infectivity risk but also a probabilistic interpretation of the risk estimation.
LAY ABSTRACT: Medicines produced from biological sources like cells can contain DNA. It is not clear what health risk the DNA can pose to the product recipients, but often it can be designed to minimize the risk by reducing the levels of DNA during manufacture. This article characterizes residual DNA risk in terms of probability, and a Bayesian approach to assessing the health risk is proposed.
1. Introdution
A variety of continuous cell lines (CCLs) have been used as substrates for the manufacture of biological products despite the fact that some CCLs are known to contain oncogenes and/or viral agents. One driving factor behind this is an economic consideration, as normal diploid cells grow slowly and often require a surface for attachment while CCLs can divide quickly in suspension (1). Because the presence of residual host cell DNA in the final product is inevitable, there is a remote possibility for the residual DNA to transmit an activated oncogene or a potentially infectious viral DNA to product recipients (2). Efforts have been made by researchers to understand oncogenic (infective) risk and risk factors (3⇓–5). Most recently, Sheng et al. (6) found that sarcomas were formed in two different mouse strains (NIH Swiss, C57BL/6) that were co-injected with 12.5 μg each of two plasmids containing either activated human H-ras or c-myc. In a related study, Peden et al. (7) discovered that residual DNA from HIV-infected cells was infectious at 2 μg. Taken together, these studies confirm the oncogenicity and infectivity of residual DNA, and they underscore the need of mitigating the risk through deactivation of the biological activity of DNA and through reduction of the amount of DNA in the final dose.
In 2006, a World Health Organization (WHO) study group on cell substrate was formed to revisit WHO requirements in light of significant progresses made in the development of biological medicinal products in novel CCLs including MDCK and Hela cell lines, as well as studies conducted at the Center for Biologics Evaluation and Research (CBER) of the U.S. Food and Drug Administration (FDA). The effort led to the recommendation of a DNA acceptable limit of 10 ng/dose (1), and this level has been widely adopted by regulatory agencies. The study group also agreed that decreasing the size of residual DNA to below 200 base pairs (bp) would further decrease the risks of oncogenicity and infectivity at the 10 ng/dose limit. The most recent publication of FDA guidance (8) states, “The risks of oncogenicity and infectivity of your cell-substrate DNA can be lessened by decreasing its biological activity. This can be accomplished by decreasing the amount of residual DNA and reducing the size of the DNA (e.g., by DNAse treatment or other methods) to below the size of a functional gene (based on current evidence, approximately 200 base pairs) …” Approximate 200 bp is currently viewed as the regulatory limit for DNA size.
In the literature, the risk of oncogenicity (infectivity) associated with residual DNA is quantified as a safety factor, which is defined as the number of doses needed to induce an oncogenic (infective) event in product recipients. Peden, et al. (7) and Krause and Lewis (9) provide two methods to estimate the safety factor (SF). As noted by Yang et al. (10), a major drawback of the two methods is that the DNA inactivation step is either not taken into account at all or not directly counted for in the estimation. Through mechanistic modeling, a new method is suggested by Yang et al. (10). This method is shown to be more accurate than the previously published methods (11). However, all the above three methods are primarily concerned with point estimation of the oncogenic or infective risk. In this article, we propose a full Bayesian procedure to assess the safety risk. Safety risk is redefined as the posterior probability for the safety factor to be above an acceptable limit. The formulation of the problem in the Bayesian framework makes it possible to incorporate the uncertainties of key parameters into the safety risk assessment. It also allows for taking full use of prior knowledge of the risk associated with residual DNA and the understanding of DNA removal processes.
2. Current Methods
Assuming that each host cell genome contains I different oncogenes of size mi, and Ii copies of the oncogene i, i = 1 … I, the total number of oncogenes I0 and the average oncogene size m are
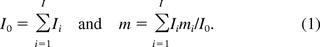
The safety factor (SF) of oncogenicity is calculated as
where Om is the amount of oncogene sequences required for inducing an oncogenic event, M the genome size or total number of DNA base pairs in one copy of the host cell, respectively, and U is the average amount of residual DNA per dose of the product. The expression
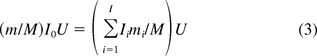in eq 3 represents the genomic mass equivalent of oncogenes in a dose. A similar formula is used for calculating safety margin of infectivity. However, the method does not take into account the effect of DNA fractionation, as the denominator in the right-hand side of eq 2 includes both fractionated and unfractionated oncogenes. As a result, the risk estimation based on this method is likely to be overstated. To correct this issue, another method was suggested by two FDA researchers, Krause and Lewis (9). In their methodology the safety factor is calculated by
where P is the percent of DNA with size greater than or equal to that of an oncogene. The formulas, establishing simple relationships between oncogenicity (infectivity) safety margins and parameters of interest, are both intuitive and easy to use. The quantities used in safety factor calculations can be either experimentally determined or extracted from the literature. We hereafter refer to these two methods as the PSPL (Peden, Sheng, Pal, and Lewis) and KL (Krause and Lewis) methods.
Recently, a new method for DNA safety assessment was developed by Yang et al. (10) based on a mechanistic modeling of the relationship between the risk and characteristics of the purification process, including DNA inactivation, and the biological nature of the host cells such as the numbers and sizes of oncogenes (infectious viral) DNA, and amounts of oncogenes (infectious agents) required to cause oncogenic (infectious) events. Key to the development of their method was to use Bernoulli and geometric distributions to describe the DNA inactivation process and the size of the DNA fragment. Let p denote the probability that the enzyme cuts phosphate ester bond between two adjacent nucleotides. The safety factor of oncogenicity is derived as
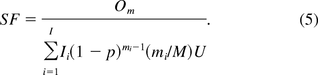A similar formula was derived for the safety factor of infectivity. It is shown that the PSPL and KL methods are special cases of the above method, under the assumptions of no DNA inactivation steps utilized in the process and one oncogene in hose cell genome, respectively (11). When the assumptions fail to hold, PSPL underestimates the safety factor while KL may either overestimate or underestimate the risk when compared to the Yang method. Because the parameters Om, U, and p are unknown, they are usually estimated based on experimental data. However, as discussed previously, all the three methods provide point estimations of safety factor without taking into account uncertainties of the parameter estimations.
3. A Bayesian Approach
3.1. Determination of Enzyme Cutting Efficiency
Consider the host cell genome DNA sequence Φ with phosphate ester bond between two nucleotides. Write Φ as
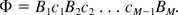
Let Z1, Z2, …, ZN* be the size of all DNA segments after enzyme digestion of Φ. Z1, Z2, …, ZN* are independently and identically distributed according to a geometric distribution P(Z = z) = (1 − p)zp. Given that each bond has probability p of being broken, imagine that the phosphate ester bonds are coded as from bond 1 to bond (M-1); see Figure 1. Because each bond has equal probability p of being cut, the number of bonds being successfully cut is a Binomial distribution Binom(M – 1,p). In other words, N*−1∼Binom(M−1,p).
Illustration of phosphate ester bonds, which are labelled as 1 to (M − 1). Each bond has probability of p to be cut by enzyme.
Now suppose that there are k genomes that go through the DNA inactivation process. The total number N of segments is the sum of segments from k genomes, each following a Binom(M – 1,p). Thus N-k ∼Binom(k(M−1),p).
Note that when the average size of DNA segments Z̄ is observed, the observed N can be replaced by kM/Z̄. In contrast, when the median size of DNA segments med0 is available, p is estimated as p = 1 − 2−1/med0 (10). However, a sampling distribution of DNA segments is not provided by Yang et al. (10).
3.2. A Bayesian Solution
Let X,Y,N denote the measurements of amount of oncogenes needed to induce an oncogenic event, measurements of amount of oncogenes in the final dose, and number of DNA segments in the final dose, respectively. It is reasonable to assume that X,Y,N are independently identically distributed according to the following distributions:
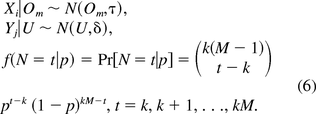Here, N(Om,τ) denotes a normal distribution with mean Om and variance 1/τ. The parameter τ is called precision, the reciprocal of variance.
Assume that the parameters in eq 6 have the following conjugate prior distributions:
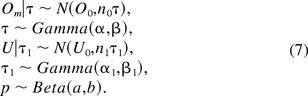It can be easily verified that the posterior distributions are:
Note that the parameters Om and U are positive real numbers. When eliciting priors, a positive restriction can be put on the normal prior distributions in eq 7, resulting in truncated normal distributions. The corresponding posterior distributions still have the forms in eq 8, but with positive restrictions in place.
Denote the parameter set θ = (Om,τ,U,τ1,p) and all the observables as X̃ = (X,Y,N). It can be easily verified that the density of the posterior distribution of θ, f(θ|X̃) is the product of the densities functions of the above five distributions in (8). Let SF0 be the acceptable lower limit of the safety factor SF. That is, the oncogenic (infective) risk of a drug product is deemed acceptable if with a high posterior probability P0 the safety factor estimate SF satisfies SF ≥ SF0. In other words,
Let I{SF≥SF0}(θ) be the indicator function of the set {θ:SF ≥ SF0}. Thus
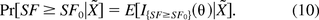
The above probability can be estimated using the following procedure: (1) Generate L random samples θ*l from the distributions in eq 8; (2) By the large number theorem,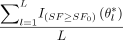 
→ E[I{SF≥SF0}(θ)|X̃] as L → ∞. Therefore the probability in eq 10 can be estimated by 
.
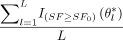3.3. An Example
Consider the following scenario: 20 experimental measurements of the amount of oncogene (μg) needed to induce an oncogenic event were taken according to the normal distribution N(9.4, 2), and the amount of oncogenes (ng/dose) in the final dose were measured 20 times following N(1,100). The mean size of residual DNA was 650. And the haploid genome size of the MDCK genome is M = 2.41 × 109 bp, and there is only one oncogene of size 1925 contained in the canine genome. The prior distributions are set as follows:
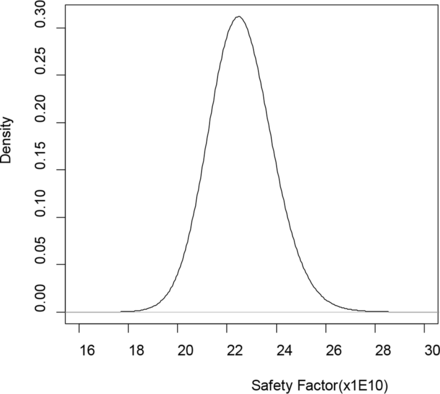
Given the priors, the posteriors in eq 8 have known distributions and random draws of 5 × 107 realizations of θ = (Om,τ,U,τ1,p) are straightforward using software packages such as R (12). Plugging in the random draws of parameters into the formula of SF gives 5 × 107 realizations from posterior distribution of SF. The mean SF is 22.570 × 109; see Figure 2 for the posterior distribution of SF based on 5 × 107 random draws. Given the lower acceptance limit SF0 = 10 × 1010 the probability in eq 10 was estimated to be 1. As a result, the oncogenic risk was considered acceptable when compared with pre-specified acceptance limit P0, say, 0.999.
Posterior distribution of safety factor (SF) based on 5 × 107 random draws.
A sensitivity analysis was conducted to ascertain whether the posterior distribution of safety factor is sensitive to prior specification. Ten scenarios were considered in Table I with various hyper-parameter specification. The hyper-parameters a and b have the least effect on the results. The safety factor was also insensitive to the hyper-parameters (α,β,α1, and β1) for precision. The most impact was found when the pair (O0,n0) or (U0,n1) was set such that the prior was informative as in the scenarios 8–10 in Table I. The posterior distribution of the safety factor changed quite a bit, although the probability Pr[SF ≥ SF0|X̃] was still above the acceptance limit of 0.999.
Sensitivity Analysis for Safety Factor under Various Priors
4. Discussion and Conclusions
The increasing use of novel continuous cell lines has driven innovation in the development and manufacturing of new biological products over the past decade. Despite purification steps during the manufacturing process, fragments of residual host cell DNA are likely present in the final product. Therefore, the oncogenic and infective risks of the cell substrates need to be carefully assessed to ensure safety of the product under development. In recent years, both WHO and FDA guidelines have been updated for the purpose of setting new standards for cell line characterization and risk assessment in light of enhanced technology, deeper understanding of various cell substrates either in use or under development, and more relevant scientific data. Although regulatory guidelines recommend limits of 10 ng/dose and 200 bp size of residual DNA in the final product, manufacturers are advised to conduct risk assessment specifically tailored to the cell substrate and product to be developed. The guidelines also stress the importance of applying risk-based methods to conduct the safety evaluations. Different limits of DNA content and size may be acceptable to the regulatory agencies if they are supported by scientific evidence and robust risk assessment. Following the mechanistic model proposed by Yang et al. (10) for the evaluation of safety risk with the consideration of enzyme digestion of residual DNA cells, this paper introduces a full Bayesian procedure for the evaluation of safety risk by incorporating the uncertainties of key parameters to allow a risk-based assessment of safety risk. It also allows for taking full use of prior knowledge of the risk associated with residual DNA and the understanding of DNA removal processes. As a result, the method not only provides a more accurate estimation of oncogenicity or infectivity risk but also a probabilistic interpretation of the risk estimation.
During the derivation of the statistical model, it is assumed that phosphate ester bonds of DNA segments have an equal chance of being cut. Practically, the chance may vary depending on the location of the bonds. For example, it is possible that the bonds on the two ends have higher probability of being broken than bonds in the middle. Such a situation needs a more sophisticated probability model such as nonhomogeneous binomial process, and it could be a future research topic.
Conflict of Interest Declaration
The authors declare that they have no financial nor non-financial competing interests related to this article.
- © PDA, Inc. 2016
