Abstract
There has been a growing interest in the assessment of container closure systems (CCS) for cold storage and shipment. Prior publications have lacked systematic considerations for the impact of dynamic time temperature transition on sealing performance associated with the viscoelastic characteristics of rubber stoppers used in container closure systems (CCSs). This paper demonstrates that sealing performance changes inherently and is fundamentally both time- and temperature-dependent. Our research results display this critical time temperature transition impact on CCS sealing performance by applying compression stress relaxation (CSR) on a rubber stopper for experimental data collection and modeling evaluation. The experimental results agree with modeling evaluation following Maxwell–Wiechert theory and the time temperature superposition based on the Arrhenius and Williams–Landel–Ferry methods. Both testing and modeling data show good consistency, demonstrating that the sealing force inevitably changes over time together with temperature transition because of the viscoelastic nature of the rubber stoppers. Our results show that compression seal force decreases quickly as temperature decreases. The significant loss of rubber stopper sealing force at lower temperature transitions could contribute significant risk to CCI at low storage and transport temperatures. Modeling evaluation, with a powerful capability to handle actual testing data, can be employed as a predictive tool to evaluate the time- and temperature-dependent sealing force throughout the entire sealed drug product life span. The present study is only applicable before reaching the rubber glass transition temperature Tg – a critical transition phase that can not be skipped/separated from real time temperature transition, and it will further determine the CCS sealing performance while approaching cryogenic temperature. The present work provides a new, integrated methodology framework and some fresh insights to the parenteral packaging industry for practically and proactively considering, designing, setting up, controlling, and managing stopper sealing performance throughout the entire sealed drug product life span.
- Compression stress relaxation (CSR)
- Residual seal force (RSF)
- Container closure system (CCS)
- Container closure integrity (CCI)
- Stopper
- Vial
- Cap
- Seal
- Capping
- Time-dependent
- Temperature-dependent
- Maxwell–Wiechert model
- Kohlrausch–Williams–Watts (KWW) stretched exponential function
- Time–temperature superposition
- Arrhenius
- Williams–Landel–Ferry (WLF)
Introduction
A popular container closure system (CCS) configuration for parenteral drug products is composed of three major packaging components: a glass vial, a rubber stopper, and an aluminum seal (1). The parenteral packaging setup includes the CCS components and the capping process. Typically, the CCS assembly is capped at room temperature, but the capped CCS assembly may have to undergo required cold-temperature processing and storage cycles after it is capped. For example, some biological drug products for parenteral administration are to be stored and shipped in the frozen state (e.g., −80°C or even lower). These low-temperature cycles may have a severely adverse impact on container closure integrity (CCI) performance (2). Currently, evaluating the sealing performance of CCSs in cold-temperature conditions is an important focus of the pharmaceutical industry. The CCS must maintain product sterility and product stability throughout its entire drug product life span. Here, the product life span is the time interval between the moment the vial is capped and the moment the patient is dosed with the sealed drug. Any CCI breach could potentially lead to oxygen, carbon dioxide, or microbiological ingress and consequently risk the drug product integrity and possibly patient health. Therefore, the rubber stopper, vial, and aluminum seal, together with the capping process, need to be properly selected and controlled to ensure CCI performance under the required cold temperature during the product life span.
A recent publication (3) provides a general overview of holistic considerations to ensure CCI performance. There are many testing methods (4⇓⇓–7) currently used to assess CCI performance. Although these CCI testing methods do evaluate CCI performance, it is well-known in the industry that residual seal force (RSF) testing (8⇓–10) can provide a complementary measurement to evaluate the actual sealed tightness of the CCS configuration. RSF is the force that a rubber closure flange exerts against the vial land seal surface of a compressed, capped CCS (3, 4, 8, 9). The resultant RSF values are directly influenced and controlled by the appropriate selection of rubber stopper, vial, and seal as assembled during the appropriate capping process setup (11⇓–13). RSF is included in USP 1207 (4) as a seal quality test for parenteral vials. Our recent publications (14⇓–16) have clearly shown that RSF is time-dependent and that it decays exponentially and eventually levels off because of inevitable relaxation of the viscoelastic nature of the rubber stoppers used in CCSs. For a given CCS configuration at lower temperature applications, it is a common practice to set up and adjust proper stopper compression through the vial capping process at room temperature and hope to obtain enough RSF for acceptable CCI performance at lower temperature. It has been reported (2) that CCI may perform adequately at room temperature but still fail at lower temperatures. There is a dearth of published documentation showing how seal force changes because of a decrease in temperature. For cold chain management in the pharmaceutical industry, it is imperative to build an impeccable understanding of the exact relationship of seal force change because of time–temperature transition and its subsequent impact on CCI performance.
Rubber stoppers are made of rubber compounds mainly composed of polymers and fillers plus some other functional additives. Rubber polymer molecular structures can be linear, branched, cross-linked, and networked, all of which affect its chemical, physical, and mechanical properties (17, 18). Rubber stoppers exhibit both elastic and viscous resistance to deformation (14, 15, 19, 20). Rubber stoppers can partially retain the recoverable (elastic) strain energy, but they also partially dissipate energy (viscous) if deformation is maintained. As reported in our previous studies (14⇓–16), RSF inevitably undergoes stress decay, known as compression stress relaxation (CSR), because of the viscoelastic nature of the rubber stopper materials (8, 14, 15). The degree of the resultant stress relaxation could have an effect on the ability of the CCS to maintain CCI throughout the entire sealed product life span.
Some physical and mathematical models, based on polymer structure and property theories, have been developed to simulate rubber stress relaxation under deformation (14, 15, 19, 20). As reported in our previous publications (14, 15), assuming a fixed compression at constant temperature, the Maxwell–Wiechert model can be modified with a nonlinear Kohlrausch–Williams–Watts (KWW) function to describe the time-dependent nature of sealing force exponential decay:
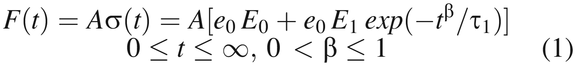where:
F = compression force;
A = compression area;
t = time;
σ(t) = compression stress at time t;
e0 = constant compression strain;
E0, E1 = elastic modulus of rubber components;
τ1 = relaxation time; and
β = KWW exponent.
Constant strain, e0, is a compression percentage determined by the capping process setup while σ(t) is the resultant compression sealing stress. The parameters E0, E1, τ1, and β are material properties associated with rubber material composition and molecule-to-molecule interactions, including molecular structures, molecular weight, molecular weight distribution, crosslinking structure, and crosslinking density, all of which affect the energy dissipated during stress relaxation. These material properties can be engineered through proper material compositions and formulations as well as during manufacturing processing.
ISO 3384-1 Rubber, vulcanized or thermoplastic — Determination of stress relaxation in compression — Part 1: Testing at constant temperature is a testing method for CSR testing (21). The compression force F(t) vs time is continuously tracked and recorded at a fixed compression percentage for the duration of the testing time without subjective human interference during the testing. Per ISO 3384-1, the dimensionless compression force ratio, Ft/Fo, is presented as a function of time, where Ft is the actual compression force measured at time t and Fo is specified as an initial compression force typically beginning 30 min after the testing has started. The Ft/Fo ratio represents the relaxation property of the rubber polymer material, and this property expression is used for the convenience of subsequent modeling considerations.
For rubber polymers, E0, E1, and τ1 are highly dependent on temperature, which affects the mobility of the rubber molecules and leads to the inevitable temperature-dependent nature of sealing force relaxation (19, 20, 22). Fundamentally, the sealing force ratio, Ft/Fo, is both time- and temperature- dependent and coupled together. The principle of time–temperature superposition (23⇓⇓–26) can be used to describe the shifting of isotherms (the sealing force ratio, Ft/Fo, found at a constant temperature) along a logarithmic time to superimpose with a reference isotherm. This means that the viscoelastic behavior at one temperature can be related to that at another temperature by a change in the time scale only (i.e., a change in temperature is equivalent to a change in the stress-relaxation rate). The ISO 11,346:2014 standard (23) describes the principle and procedure for the time–temperature superposition used both by industry and in the academy, and it presents two notably different methods, namely the Arrhenius and Williams–Landel–Ferry (WLF) methods. These two different approaches are the most popular methods of time–temperature superposition calculations for stress relaxation. The established time–temperature superposition for viscoelastic rubber stopper materials is not valid for the same viscoelastic rubber material below its glass transition temperature because the viscoelastic rubber material will be vitrificated because of freezing of the rubber molecule segment motion, whereby it will become a rigid solid material with very different properties in a physical sense. However, viscoelastic rubber stopper material has the memory capability to resume its time–temperature superposition track once the temperature returns above its glass transition temperature. Subsequently, its rubber molecule segment motion is resumed as well (19, 20, 22).
The Arrhenius principle describes how the rate of a polymer property can change with temperature, such as choosing the Ft/Fo ratio as the relaxation property. By exposing test samples to a series of different temperatures, the relationship between temperature and the relaxation property (Ft/Fo ratio) change rate can be found. This property change rate/temperature relation is represented by the Arrhenius equation:
where, k(T) is property change rate, C is a constant, Ea is the activation energy (kJ/mol), R is the gas constant (J/mol·K) and T is the absolute temperature (K). At a specific test temperature, the change rate of a chosen property Ft/Fo ratio value is determined as a function of time – CSR. Testing is continued for a long enough period until the relevant threshold of that property Ft/Fo ratio value has been exceeded, so that the time-limit t1 for that temperature T1 is determined. The threshold value should be chosen to suit the realistic testing conditions. Further testing must be carried out at no less than two different temperatures for a total of no less than three different temperatures. The time limits (t1, t2, t3, … …) obtained at the threshold for each temperature (T1, T2, T3, … …) are plotted on an Arrhenius chart as a function of the temperature. The time-limit data points (t1, t2, t3, … …) are expressed in log time. The log time at which the threshold value is reached for each of the test temperatures is plotted against the reciprocal 1/T of the corresponding temperature. Per ISO 11,346:2014 standard practice, a typical Arrhenius chart has the log time ln(t) as a vertical axis against 10,000/T as a horizontal axis. A best-fit straight line through the plotted points can be constructed by linear regression with an empirical mathematic expression:
where a1 and a2 are parameters to be determined by linear regression. The straight regression line through these points can be extrapolated back to the temperature point of intended service temperature. The Arrhenius method is typically used for property change rate associated with chemical degradation as well as physical aging.
Another approach to seek the relationship between temperature change and the polymer property (Ft/Fo) change rate is by the WLF method. The WLF method is applicable to the physical aging of a viscoelastic material. WLF states that the effect of temperature change on the property (Ft/Fo) change rate is equivalent to applying a shifting factor a(T) to the time scale defined as follows:
In this expression, a(T) is an intermediate variable called the shifting factor of the Ft/Fo relaxation curve determined at temperature T in relation to the reference temperature Tref, typically chosen at 23°C or any other temperature. The constants C1 and C2 are both rubber polymer structure and temperature-dependent. Eq 4 can be expressed as:
Per ISO 11,346:2014 standard practice, standard curve fitting techniques can be used for eq 5. However, eq 4 can also be expressed as:
Eq 1 can be assumed under an isothermal condition of reference temperature Tref at time tref. Substituting eq 6 into eq 1 for time shifting, it becomes:
Basically, as a continuation of our previously published study (14, 15), eq 7 is based on the Maxwell–Wiechert model modified with a nonlinear KWW function for time-dependent compression relaxation and combined with time–temperature superposition considerations by adopting a WLF shifting factor format. For experimental verification of modeling eq 7, simply run a compression test by tracking Ft/Fo against time (t) change and temperature (T) change followed by numerical modeling fit for eq 7. Typically, the reference temperature Tref is set at a constant 23°C, or it can be at any specific temperature of interest.
After some mathematic maneuvers for explicit expression, the time–temperature-dependent eq 7 becomes:
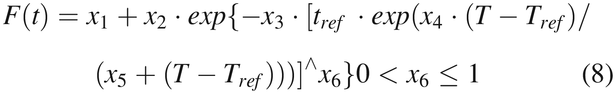where x1, x2, x3, x4, x5, and x6 are the parameters adopted to represent Αe0E0, Ae0E1, 1/τ1, C1, C2, and β, respectively. The numerical modeling evaluation with the actual test data can be carried out using numerical nonlinear method (13, 14, 26⇓–28) by systematic iterations for the minimization of:
where Ft(t) is the testing observed force and Fm(t) is the modeling force. F(x) is nonlinear. The numerical method here is to solve the partial differential equation matrix:
by following numerical iterations:
Once all the final values (x1, x2, x3, x4, x5, and x6) have reached and satisfy ||(∇F(x))|| < ε,, the numerical modeling evaluation is complete. Modeling evaluation (14, 15, 27⇓–29) based on eqs 9–12 can process a massive amount of testing data simultaneously from multiple testing curves collected from the same testing setup. Dividing F(t) by Fo, it becomes an Ft/Fo modeling evaluation.
To investigate further, this study investigates the coupled time- and temperature-dependent impact on the rubber stopper sealing force. Particularly, we examine: (1) CSR testing at different temperatures to experimentally explore coupled time–temperature dependence, especially during low-temperature transition; (2) time–temperature superposition for its consistency with testing results and predictability; and (3) modeling evaluation for simulation and prediction of sealing force relaxation through a low-temperature transition over time. In general, the mandatory regulatory requirement is that sterile pharmaceutical products remain sterile and that stability is maintained over the sealed drug product life span. This implies that CCI must be maintained during low-temperature transitions as well as during the sealed drug product life span. The main goal of this study is to raise much-needed awareness of the time–temperature transition impact on CCS sealing performance over a sealed drug product life span for patient safety. The time–temperature superposition methodology can be used as a predictive investigation tool by readers to generate their own evaluations of their specific CCS configuration scenarios to satisfy the required sealing performance at intended temperature transition conditions throughout the entire sealed drug life span.
Experimental Testing Setup
The CSR testing setup is per ISO 3384-1:2011 Rubber, vulcanized or thermoplastic — Determination of stress relaxation in compression — Part 1: Testing at constant temperature. A testing setup (Figure 1) is composed of a 20 mm rubber serum stopper plugged into a stainless-steel fixture designed to dimensionally mimic a 20 mm glass vial (flange/neck/shoulder) with an aluminum seal covering the stopper. The testing machine is calibrated for its loadcell with temperature window before testing. The aluminum seals are not crimped onto the stainless-steel vial fixture. The entire sample assembly is compressed between two flat metal plates within a testing chamber. The compression percentage is maintained at a fixed 25% compression of the stopper flange thickness or at any other fixed compression percentage desired. The testing temperature can be programmed and controlled for specified time and temperature transition cycles within the testing chamber. The compression force vs time vs temperature is continuously monitored for the duration of the testing. The following is a summary of the CSR testing setup:
The testing chamber can be programmed and controlled for the specified time and temperature cycles.
Six samples are tested in the testing chamber at the same time for each testing set.
Samples are 20 mm serum rubber stoppers with a nominal flange thickness of 3.30 mm. All the testing samples have the same rubber material composition.
A stainless-steel fixture is designed to dimensionally mimic a 20 mm glass vial (flange/neck/shoulder) holding a 20 mm stopper as shown in Figure 1. All testing sample assemblies are covered with aluminum seals but not crimped onto the 20 mm stainless steel fixture.
A 20 mm West aluminum I-seal is used.
All testing samples are subject to a fixed 25% compression of the stopper flange thickness throughout the entire testing duration. The 25% compression is precisely controlled and maintained by the testing machine.
All testing samples are conditioned in the testing chamber at the specified testing temperature for 24 h prior to starting the compression for the testing. The 25% compression is applied and maintained starting at the time zero of the testing.
The compression force vs time vs temperature is continuously tracked and recorded by computer throughout the entire duration of the experiment without subjective human interference. Fo is specified as an initial compression force beginning 30 min after the time zero. The compression-relaxation property (Ft/Fo ratio) is continuously displayed and monitored during the testing.
Testing setup for compression stress relaxation.
Experimental Testing and Modeling Evaluation Results and Discussion
Our study includes the following:
CSR testing for time- and temperature-dependent experimental data collection.
Time–temperature superposition evaluation.
Modeling evaluations for time–temperature transition and its impact on sealing performance.
At a fixed 25% compression of the stopper flange thickness, the CSR test data at 23°C is displayed in Figure 2, in which Ft/Fo is the compression relaxation ratio data per the ISO 3384-1 standard method. Figure 2A,B are displayed with exactly the same testing data but their horizontal time axes are in nonlogarithmic time vs logarithmic time. The average Fo of six testing samples is 73 N. The compression relaxation ratio Ft/Fo captures and represents the relaxation properties of the rubber polymer material per the ISO 3348-1 standard method. Our study uses the Ft/Fo property data to investigate the time–temperature transition nature of sealing performance. Evidently, all testing curves in Figure 2 consistently demonstrate time-dependent exponential decay that eventually levels off as expected because of the viscoelastic nature of the rubber stoppers. The Ft/Fo testing data reached the 80% threshold for this rubber stopper material after more than eight weeks (1400+ h).
(A) Compression stress-relaxation testing results at 23°C isotherm temperature (horizontal axis in nonlogarithmic time). (B) Compression stress-relaxation testing results at 23°C isotherm temperature (horizontal axis in logarithmic time).
Figure 3 shows the compression relaxation ratio Ft/Fo of CSR testing data at isotherm 23°C, 0°C, −20°C, −40°C, and −50°C, respectively, with 80% Ft/Fo threshold. Six data curves overlap for each temperature setting for a total of 30 data curves for five different isotherm temperature settings. The Ft/Fo curves clearly demonstrate stress relaxation acceleration with a fall in temperature. The stress relaxation acceleration is significant because it is represented on a logarithmic time scale. The rationale for stress relaxation acceleration at lower temperature is likely because of rubber stopper shrinkage at lower temperatures, but this hypothesis will be further investigated in a later study. Rubber stopper shrinkage at lower temperature was visually observed and reported previously (30, 31). Here, our CSR testing data curves are showing significant losses of sealing force at lower temperature in terms of the time–temperature transition of the viscoelastic rubber material.
Compression stress-relaxation testing results for different isotherm temperatures.
The Arrhenius time–temperature superposition is calculated per the ISO 11,346:2014 standard method (23) by shifting the isotherms of Ft/Fo testing results from Figure 3. Figure 4 is the Arrhenius plot. In Figure 4, the log time at which the 80% threshold value is reached in Figure 3 for each test temperature is plotted against the reciprocal 1/T of the corresponding absolute temperature in kelvin. Figure 4 also includes a best-fit straight line, and its equation through the plotted data points is constructed by a linear regression equation per eq 3.
Arrhenius plot (time against temperature).
Per the Arrhenius time–temperature superposition method, the Ft/Fo at one temperature can be quantitatively related to Ft/Fo at another temperature by a simple change in the time scale along the straight line in Figure 4. Using Ft/Fo results at 23°C as a reference, we can calculate and predict Ft/Fo results at other temperatures. Thus, Figure 5 includes the calculated/predicted Ft/Fo master curve (red legend line) at the 23°C reference temperature and all other Ft/Fo testing curves at different temperatures shifted toward the master curve at 23°C. These curves match relatively well when superimposed on one another at 23°C. This good match is not surprising because the linear regression is in line with the actual testing data points in Figure 4. By the same token, the master curve can be used to calculate and shift the Ft/Fo ratio data from the 23°C reference temperature to any other temperature for Ft/Fo ratio prediction. For instance, Figure 5 includes a calculated/predicted Ft/Fo ratio curve (black legend) at −30°C, which is shifted from the master curve.
Master curve and shifted testing data curves at 23°C reference temperature and predicted relaxation curve at −30°C, all based on Arrhenius method.
In a parallel approach, the WLF time–temperature superposition is also calculated per the ISO 11,346:2014 standard method (23) by shifting the isotherms of Ft/Fo testing results from Figure 3. Figure 6 is the WLF plot, in which the time-limit data points are collected from Figure 3 at the 80% Ft/Fo threshold, and the intermediate shifting factor variable ln[a(T) exp] is calculated by the equation ln[a(T) exp] = ln(tref/t) per eq 4 with reference temperature Tref = 23°C. In Figure 6, per the WLF method, −1/ln[a(T)exp] is plotted against the reciprocal 1/(T − Tref) of the corresponding temperature in degree Celsius. A best-fit straight line and its equation through the plotted data points is constructed by linear regression equation per eq 5.
Shifting factor a(T) fitted by the William–Landel–Ferry (WLF) method.
The shifting factor a(T) established by the linear regression equation in Figure 6 is also expressed in Figure 7 by plotting log [a(T)] against temperature T, and it is used for subsequent master curve calculation.
William–Landel–Ferry (WLF) shifting factor a(T) plot.
Applying the same method for Figure 4, the WLF results in Figure 6 imply that the Ft/Fo at one temperature can be quantitatively related to Ft/Fo at another temperature by a simple change in the shifting factor along the straight line in Figure 6. It allows us to generate a compression-relaxation ratio Ft/Fo master curve at the 23°C reference temperature. Figure 8 shows the calculated Ft/Fo master curve (red legend line) at the 23°C reference temperature based on the WLF method. By using the time–temperature superposition in Figure 6 and the WLF method for tref = t · a(T) defined in eq 4, all other Ft/Fo testing curves at different temperatures can be calculated and shifted toward the master curve at the 23°C reference temperature as displayed in Figure 8. The master curve can also be used to calculate and shift the Ft/Fo ratio data from the 23°C reference temperature to any other temperature for Ft/Fo ratio prediction. Figure 8 includes a calculated/shifted/predicted Ft/Fo ratio curve (black legend) at −30°C.
Master curve and shifted testing data curves at 23°C reference temperature and predicted relaxation curve at −30°C, all based on the William–Landel–Ferry (WLF) method.
A CCS is typically assembled during a capping process at room temperature. The assembled CCS may then need to withstand lower temperature conditions either per drug processing requirement and/or drug storage and shipping requirements, and the CCS may be returned to room temperature for dosage injection. As a significant step forward in a practical sense, Figure 9A shows a case study of CSR testing at fixed 25% compression on the exact same rubber stopper material for a total of six samples, but testing chamber temperatures were programmed to include some fluctuating temperature cycles in real time back and forth between 23°C and −65°C in addition to the 23°C reference temperature baseline. Figure 9A also includes modeling fit results (red legend) based on eq 7 using the testing data from these six samples. The results in Figure 9A are powerful and revealing. They provide fundamental insight into the puzzle of CCI performance loss at lower temperatures, which has been an issue for the parenteral drug industry for a long time. Here are the major highlights for the results displayed in Figure 9A:
As expected from the early results of this paper, the compression-relaxation ratio Ft/Fo decreases as temperature decreases and vice versa for testing temperatures between 23°C and −65°C.
The rationale for the decrease in the compression-relaxation ratio Ft/Fo along with a fall in temperature is because of temporary shrinkage of the rubber stopper at lower temperatures, which is empirically supported by other experimental observation and documentation (30, 31). However, this shrinkage rationale needs to be further investigated in a later study. In general, material temperature is a function of the average molecular kinetic energy of a rubber polymer material (17⇓⇓–20, 22). When the rubber polymer material is heated, the kinetic energy of its molecules increases. Thus, the molecules begin vibrating and moving more and usually maintain a greater average separation because of thermal expansion. This temporary rubber material expansion is reversible once the temperature decreases and causes shrinkage.
Figure 9A includes two modeling results from the exact same modeling equation.
The original modeling equation in red font has both time t and temperature T as variables for the time–temperature transition to capture temperature cycling, and it matches relatively well with the testing results of the time–temperature transition. Any visible deviation between testing data and modeling data may be because of imperfections in dynamic temperature control in the testing chamber and how close the recorded chamber testing temperature was to the actual rubber stopper material temperature. This rubber stopper material's glass transition temperature Tg is −61.12°C, tested per the ASTM D7426 Standard Test Method for Assignment of the DSC Procedure for Determining Tg of a Polymer or an Elastomeric Compound. The time–temperature superposition modeling evaluation is only applicable to rubber stopper material in a viscoelastic status, not beyond the material glass transition temperature. The testing temperature cycle in Figure 9A reaches −65°C, lower than the −61.12°C material glass transition temperature. This might explain why slightly more deviation between testing data and modeling data is seen in Figure 9 during the temperature cycle at −65°C.
The original time–temperature transition modeling equation (red font) in Figure 9A can be used to predict CSR at different temperature cycles. By setting T = 23°C in the original equation, the modeling equation (purple font) predicts an isotherm at the 23°C reference temperature, essentially in the format of eq 1. It clearly demonstrates exponential decay (time dependent only) as expected because of the viscoelastic nature of the rubber stoppers, which eventually levels off. The modeling curve matches well with the testing data curves assuming an isotherm temperature of 23°C.
After going through temperature cycling, the compression-relaxation ratio Ft/Fo has memory capability to return from −65°C to its time-dependent relaxation track at the isotherm 23°C reference temperature baseline, as shown in Figure 9B. All the data curves in Figure 9B are exactly the same as in Figure 9A, except they are represented in logarithmic time scale to capture the exponential Ft/Fo decay of the 23°C isotherm baseline. Apparently, the rubber stopper regains its sealing force and reseals the CCS after rewarming to ambient temperature. More importantly, it must be pointed out here that if all the CCI testing is done at room temperature before and after the cooling cycle, depending on the CCI testing method used, it may or may not be able to capture the possible leakage damage already done to the drug during the cold temperature cycle.
For this particular rubber stopper, Figure 9A,B clearly shows that lower temperature decreases in sealing force are much more significant than time-dependent relaxation and cause more noticeable adverse impact on sealing performance.
(A) Compression stress-relaxation testing and model results through different temperature cycles (horizontal axis in nonlogarithmic time). (B) Compression stress-relaxation testing and model results through different temperature cycles (horizontal axis in logarithmic time).
In summary, the seal force of a CCS will inherently change while undergoing time–temperature transitions, with the potential for a severe loss of seal force at lower temperatures. CCSs will experience CSR because of both time- and temperature-dependent viscoelastic properties determined by the rubber formulation and the rubber stopper manufacturing process. In addition, the viscoelastic properties of rubber stoppers may be affected by the washing process, the sterilization process, low-temperature processing and conditioning, drug contact, shipping through different climates and/or elevations, low-temperature storage conditions, use-and-reuse in multidose applications, and other processes, all of which may influence the CSR of rubber stoppers during time–temperature transition. Good rubber stopper properties are required for acceptable CCS configurations assembled with a proper capping process setup to maintain a seal force that will ensure CCI performance throughout the entire sealed drug product life span. By using the integrated framework laid out in this study, more scenarios are to be further iterated and conducted for future case studies and later publications.
Conclusion
This study conducted CSR testing and modeling evaluation of rubber stoppers used in CCSs. The testing setup for the study is per the ISO 3384-1 standard testing method for experimental data collection. The seal force of a CCS will inherently change when undergoing time–temperature transitions, with a significant loss of seal force at lower temperatures that could adversely affect CCS sealing performance. As demonstrated through this study, the significant loss of rubber stopper sealing force at lower temperature transitions could contribute significant risk to CCI at low storage and transport temperatures. The CSR accelerates at lower temperatures because the rubber stopper shrinks more significantly at lower temperatures, and more research is needed to further understand the impact of rubber shrinkage on CCS sealing performance at lower temperatures. The CSR is quantitatively predictable with the time–temperature superposition either by the Arrhenius method or the WLF method. A nonlinear CSR model is developed based on the Maxwell-Wiechert model modified with a KWW function and combined with time–temperature superposition by adopting a WLF shifting factor format. Employing both experimental evaluation and modeling calculations on a 20 mm CCS, the results demonstrate that the testing and modeling data show good consistency. The modeling capability to handle actual testing data can be employed as an investigation tool to calculate and predict the inevitable change in seal force throughout the entire sealed product life span during time–temperature transition. The present study is only applicable before reaching the rubber glass transition temperature Tg – a critical polymer phase transition that cannot be skipped/separated from real time–temperature transition, and it will further determine the CCS sealing performance while approaching cryogenic temperature. Our future research will include the dynamic time–temperature transition impact on CCI sealing performance beyond the glass transition temperature.
Conflict of Interest Declaration
The authors declare that they have no competing interests.
Acknowledgments
Thanks to Greg Warner for testing equipment installation and setup, to Brad Gasser for computer data acquisition setup for testing, and to Tom Coccia and Mark Lacek for their design and machining of some fixture parts used in this study.
- © PDA, Inc. 2020
References
In This Issue
Jump to section
Related Articles
Cited By...
More in this TOC Section
Similar Articles
Keywords
- Compression stress relaxation (CSR)
- Residual seal force (RSF)
- Container closure system (CCS)
- Container closure integrity (CCI)
- Stopper
- Vial
- Cap
- Seal
- Capping
- Time-dependent
- Temperature-dependent
- Maxwell–Wiechert model
- Kohlrausch–Williams–Watts (KWW) stretched exponential function
- Time–temperature superposition
- Arrhenius
- Williams–Landel–Ferry (WLF)